Multiwave Oscillator Impedance – Part 1

7th January 2019

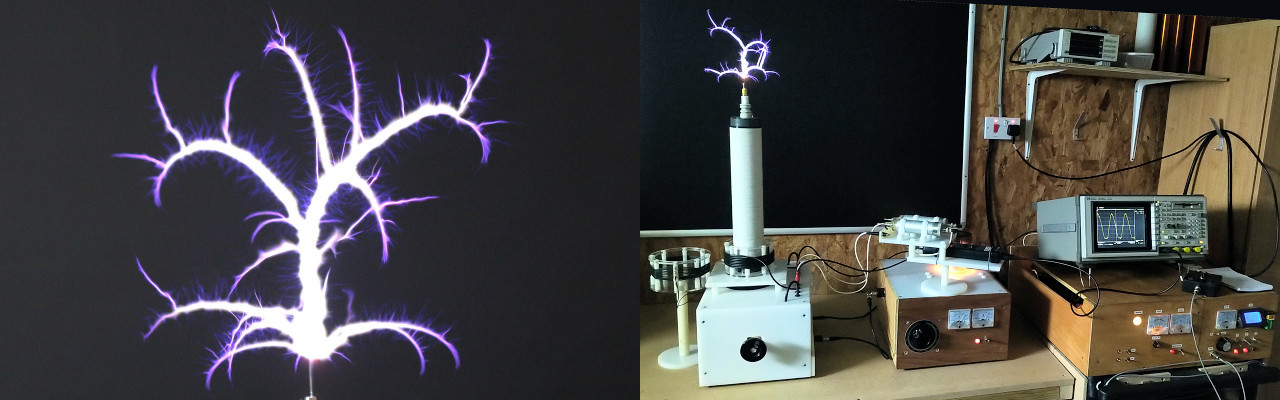
The original Lahkovsky Multiwave Oscillator (MWO) apparatus combines two Tesla style drive coils in a transmitter and receiver configuration, each consisting of a primary and secondary coil cylindrically mounted on axis. The top-load for both transmitter and receiver is a complex combination of concentric half-wave resonators. The impedance characteristics of even a single drive coil with top-load represents a complex measurement challenge with results that can span over a very wide frequency range, in the order of 100kc/s – > 1Gc/s.

In this first part the small signal impedance characteristics, Z₁₁ (magnitude and phase) with frequency as seen by the generator, are measured for a single drive coil both with and without the MWO top-load over the lower frequency range of 100kc/s – 20Mc/s. In this measurement the impedance characteristics are dominated by the drive coil which will mask any higher frequency measurements pertaining to the MWO top-load. For this reason the top-load is measured individually in part 2 in the frequency range 100kc/s – 1.3Gc/s. Subsequent parts will look at the overall MWO system impedance characteristics when both transmitter and receiver are combined together in the original Lahkovsky arrangement, and later in an optimised and balanced drive arrangement as designed and presented by Dollard^[1].

In this first part the following measurements are presented:

1. Z₁₁ (magnitude and phase) with frequency for a drive coil without MWO top-load in the range 100kc/s – 20Mc/s

2. Z₁₁ for the drive coil combined with MWO top-load, and over the same frequency band.

3. Primary tuning measurements to match the resonant frequency of the primary coil, (with series loaded Cp), to the secondary coil at the fundamental, second, and third harmonics.

The SDR-Kits Vector Network Analyser 3E (VNA-SDR) was used to make all Z₁₁ measurements, and the apparatus and method of measurement is shown in Figures 1 below.

Fig. 1.1 Experimental setup for the MWO TC drive Z₁₁ impedance measurements, showing the TC drive coil, VNWA-SDR, calibration modules, and connection to the computer.
Fig. 1.2 The TC drive coil is connected via a pcb feed adapter to the VNWA-SDR via a short SMA RG178 coaxial cable.
Fig. 1.3 The TC drive adapter pcb is arranged to feed the TC via an SMA connector which allows for a calibrated series capacitance to be connected, and hence different resonant tuning points between the primary and the secondary.
Fig. 1.4 The feed pcb enables the VNWA-SDR calibration to extend right to the input terminals of the TC, eliminating spurious measurement effects from the connectors, cables, and geometry.
Fig. 1.5 The pcb feed adapter is calibrated in stages against a standard short circuit, open circuit, and 50Ω load. The series capacitance connector is here shorted with an SMA short when not being used.
Fig. 1.6 Here the feed pcb is connected to both the VNWA-SDR and a calibrated series capacitance box Cs. With both connected the VNWA was first calibrated using the three standard loads with Cs set to 1uF.
Fig. 1.7 The TC drive coil connected with MWO topload and measured in the same way as before to compare the impedance loading effects.
Fig. 1.8 The MWO topload is connected directly to the TC drive coil via short copper spacers where one end is driven from the secondary coil output, and the other open circuit, forming a λ/4 or shorter driven outer ring.

To view the large images in a new window whilst reading the explanations click on the figure numbers below.

Fig 1.1. Shows the overall measurement setup with the VNA-SDR connected to the drive coil by a short SMA terminated RG316 cable, and the other end to the coil feed adapter, and standard calibration modules.

Fig 1.2. The drive coil used in these measurements has 4.5 primary turns of AWG 10 ~2.5mm diameter magnet wire, and the secondary has 248 turns of AWG 24 ~0.51mm diameter magnet wire. The top-end of the primary coil is connected directly to the bottom-end of the secondary coil and forms the negative or ground terminal. The positive or drive terminal is connected to the bottom-end of the primary coil, and the top-end of the secondary can be seen emerging from the coil through a brass bolt which attaches to the driven top-load. Both coils are wound anti-clockwise on the former from the base.

Fig 1.3. In order to make an accurate measurement of Z₁₁ it is necessary to calibrate the VNA-SDR as close to the drive coil as possible. In this case the calibration plane is extended to the input of the primary coil terminals, (two 4mm high voltage shielded terminals), via a signal feed adapter pcb (SFA). The SFA can be removed from the drive coil by drawing the two-pronged 4mm probes out of the drive coil terminals. With the SFA disconnected the VNA-SDR can be calibrated by fitting an open, short and 50Ω standard load to the end of the SFA. The effective calibration plane then becomes the input to the drive coil, and spurious impedance effects due to any cables and the SFA itself can be removed from the final results. When calibrated, a frequency scan of the SFA with the 50Ω standard load will show a flat impedance line for |Z|, (magnitude of the impedance). The phase of this scan will swing repeatedly between ±180° indicating the near perfect match between the calibration plane and the 50Ω standard load.

Fig 1.4. Shows a close-up of the SFA connected directly to the two high voltage drive terminals in the base of the drive coil. The SFA has an SMA input feed and is then connected via equal weights of copper to the series connection point. The black terminal indicates the negative or ground point where both primary and secondary are connected together, and the red terminal the high voltage feed end of the primary. The series connection point in the positive terminal allows for a calibrated capacitance box to be connected in the primary circuit for tuning measurements. In this picture the series connection is not being used and is terminated with a SMA short. In tuning measurements, when series capacitance C_S is added, the SFA must first be calibrated with the capacitance box connected to the SFA with a nominal 1µF set at its output. The 1µF series capacitance has a very low impedance at the measurement band of interest and acts effectively as a short-circuit of the series connector during the calibration procedure. During tuning measurements the capacitance of the box is reduced in the range 100pF – ~ 50nF. The capacitance box itself uses surface mount standard capacitance values and can be reasonably used with SMA connection up to ~ 100Mc/s. The SFA is an unbalanced feed adapter and takes an unbalanced coaxial cable input directly to a balanced two terminal output without any compensation for this change in balance. A similar SFA was also tried which incorporated an RF (upto ~ 3Gc/s) balun in order to effect the transformation between the unbalanced and balanced connections. However, even with calibration the balun SFA proved to be less effective to measure Z₁₁ accurately and cleanly, as it dominated the impedance changes in the frequency band masking changes due to the drive coil further downstream. The standard SFA was therefore used with careful calibration up to the intended reference plane at the input terminals to the coil.

Fig 1.5. Shows the calibration procedure where the SFA is connected in turn to the standard calibration modules, here connected to the short circuit module. In this case the series capacitance terminal is not being used and is shunted with an SMA short.

Fig 1.6. Shows the SFA in measurement configuration and after calibration, where a 1nF series capacitance is added to the primary feed. The calibrated capacitance box can be adjusted in 1pF increments in the range ~30.5pF – ~10µF, where the parasitic capacitance of the box with SMA cable and when set to zero is ~30.5pF.

Fig 1.7. Shows the overall measurement setup with the top-load connected, and then calibrated and measured in the same procedure as previously discussed. The outer ring of the top-load forms an effective wire extension and capacitive load to the top of the secondary coil, which will both reduce considerably the fundamental resonant frequency and Q-factor of the drive coil. When compared with the drive coil without top-load the outer ring forms a λ/4 driven ring, which is coupling to 11 other λ/2 resonating rings. Given the size of the outer driven ring, and the proximity of the inner rings the coupling factor is considered to be quite high between the driven ring and the inner resonators, which will tend to constrain the free resonation of the inner rings and considerably quench the Q and hence measurements at much higher frequency. This is considered more closely in part 2.

Fig 1.8. Shows in more detail the mounting points at the top-end of the secondary and the MWO top-load.

Figures 2 below show the Z₁₁ impedance characteristics of the calibrated reference plane, the drive coil, and primary and secondary tuning with series added capacitance, of the drive coil only.

Fig. 2.1 Calibration results for the 50Ω standard load over the measurement window of 100kc/s - 20Mc/s. This calibration takes into account the TC feed pcb and a series capacitance Cs = 1uF, creating a calibrated reference plane at the TC input connectors.
Fig. 2.2 Magnitude and phase for Z11 showing the fundamental resonant frequency of the TC at M1 (1.28Mc/s), and many harmonics, (the VNWA-SDR software allows for a maximum of 12 simultaneous marker points).
Fig. 2.3 Narrowband calibration for Z11 against the 50Ω module over the range 100kc/s to 5Mc/s, to measure with greater detail the fundamental resonant frequency, 2nd, and 3rd harmonics.
Fig. 2.4 The fundamental resonant frequency, 2nd, and 3rd harmonic for the TC drive with a series primary capacitance Cs = 1uF, (very low impedance across the band).
Fig. 2.5 The series capacitance in the primary reduced to 400pF to show the 180° phase change in the primary that occurs at resonance (M4), and the accompanying very low series resistance at resonance.
Fig. 2.6 Cs has been increased to 540pF where the resonant frequency in the primary matches the resonant frequency of the 3rd harmonic of the secondary at M4 (4.31Mc/s). The matched primary and secondary resonance cause frequency splitting in Z11 at M3 and M5.
Fig. 2.7 Cs is further increased to 1200pF where the primary and secondary match now occurs at the 2nd harmonic M3 (2.95Mc/s).
Fig. 2.8 The primary and secondary resonance now match at the fundamental resonant frequency at M2 (1.28Mc/s), and Cs = 6500pF. When driven by a non-linear generator such as a spark gap the primary would resonate predominately at M1 (1.17Mc/s) with many other harmonics and beat frequencies present.

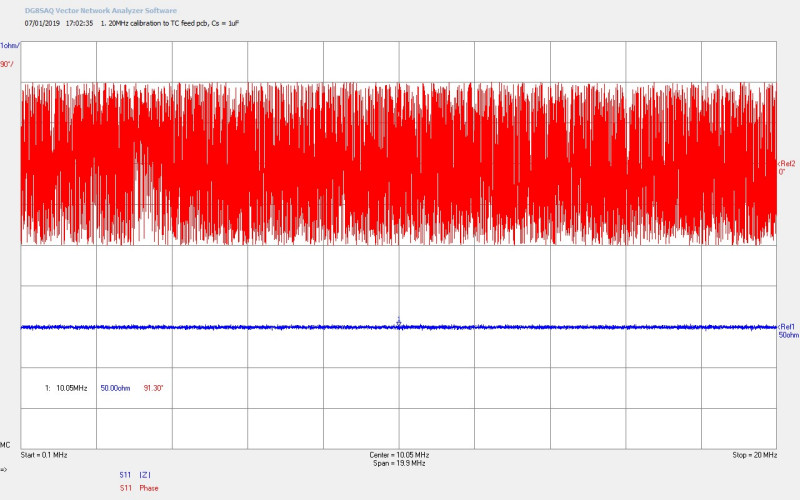
Fig 2.1. Shows the calibrated reference plane of the SFA when connected to the 50Ω standard load over the wideband range 100kc/s – 20Mc/s. The calibration is as expected and accurate over the band, with a slight phase variation between ~ 3 – 3.5Mc/s indicating a resonance in the signal path between the calibration plane and the VNA-SDR which has been normalised out by the calibration procedure.

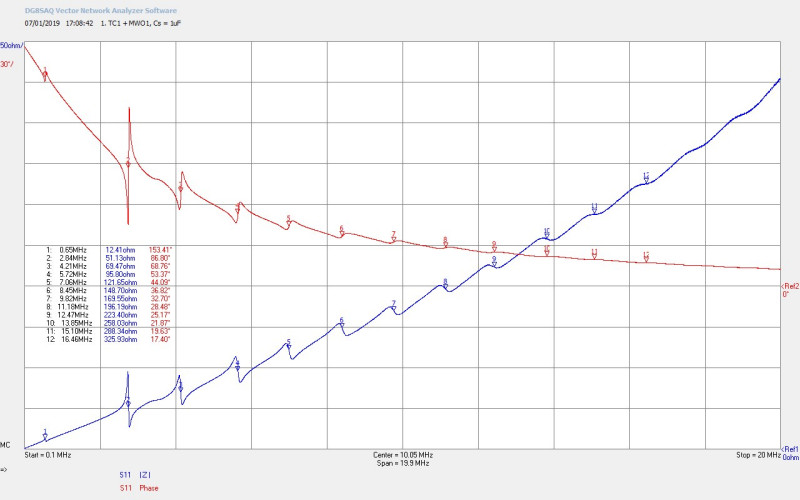
Fig 2.2. The impedance characteristics of the drive coil with the series capacitance Cs = 1µF, showing a wealth of resonant peaks and corresponding phase changes from the fundamental resonant frequency F_S of the secondary coil at 1.28Mc/s up to the 12th harmonic F_S₁₂ (M₁₂) at 16.51Mc/s. It is interesting to note that the 2^nd harmonic F_S2 at M₂ is a stronger resonance than that of the fundamental at M₁. This is further demonstrated in subsequent impedance results. The VNA-SDR allows for only 12 concurrent markers which is why the final two harmonics on the results are not marked. At frequencies above 20Mc/s the rapidly increasing inductive impedance of the primary masks out any further harmonic points of interest, and the impedance curve rises rapidly until the primary coil becomes self-resonant at ~38Mc/s.

Fig 2.3. Shows the calibrated reference plane of the SFA when connected to the 50Ω standard load over the narrowband range 100kc/s – 5Mc/s. With more accurate calibration in the narrowband it can be noted that the phase variation seen in Fig. 2.1 has now been completely normalised out of the reference plane.

Fig 2.4. Shows the narrowband impedance characteristics for the fundamental F_S and the first two harmonics F_S2 and F_S3. Here the difference in magnitude of the resonance between F_S and F_S2 can be very clearly observed, although the Q of the coil remains very similar for both frequency points. The magnitude of the impedance |Z₁₁| ~ 28.5Ω at F_S, and ~ 49.7Ω at F_S2would significantly impede currents developed in the primary from the generator, coupling very little power to the secondary and ultimately to the MWO top-load. The primary circuit will need to be brought into resonance with the secondary at the corresponding frequency in order to considerably reduce the driving impedance seen by the generator, and hence maximise the primary currents, and the amount of power transferred from the generator through the drive coils to the top-load. On the very far left of the scan at 100kc/s the 180° phase change F_Ø180 of the primary in resonance with the series capacitance C_S can just be observed. This will be adjusted by varying C_S in subsequent results in order to tune the primary resonant frequency to that of the secondary. Given the difference in magnitude between the fundamental at F_S and the 2^nd harmonic at F_S2 it may be more optimal to arrange the primary to resonate at F_S2 rather than the fundamental for normal experimental operation. This will be tested during experiments and reported in subsequent parts.

Fig 2.5. Here the series capacitance C_S has been reduced from 1µF to 400pF which has increased F_Ø180 (the resonant frequency of the primary to M₄ at 4.93Mc/s. At this point the impedance seen by the generator has reduced drastically to ~0.72Ω allowing for much larger primary currents. In this case F_Ø180 does not correspond to a resonant frequency in the secondary so reduced power would be transferred between the two coils. At lower frequencies in the measurement band, the impedance of C_S is higher and has the effect of attenuating currents in the primary reducing considerably the magnitude of the lower resonant points, in this case considerably suppressing the fundamental resonance at F_S. This scan clearly shows the effect of including a series resistance in the primary and making it resonant within the measurement band of interest.

Fig 2.6. Here C_S has been increased to 540pF which has brought the resonant frequency of the primary equal to the 3^rd harmonic resonance of the secondary at M₄at 4.31Mc/s. As always with coupled resonant circuits, mixing of the signals causes beat frequencies and hence frequency splitting into two sideband frequencies where the impedance minimum points are at both the lower and upper resonant frequencies F_L3 (M₃) and F_U3 (M₅) respectively. If driven by a generator with C_S = 540pF F_L3 would be the best driving point since proximity coupling to the secondary top-load, or discharge of stored energy on the top-load, would momentarily increase the loading on the coil reducing slightly its secondary harmonic frequency towards F_L₃, and hence maximising transference of electric power between the primary and secondary coils.

Fig 2.7. Shows C_S increased further to 1200pF which now tunes the primary resonance to the 2^nd harmonic F_S2 at M₃ a frequency of 2.95Mc/s. Again frequency splitting occurs and the impedance of F_L2 and F_U2 are very low ~0.5 – 1Ω facilitating high current drive from the generator.

Fig 2.8. Shows C_S finally increased to 6500pF which tunes the primary to the fundamental resonant frequency of the secondary F_S at M₂ at 1.28Mc/s. At F_L (M₁) the lowest impedance drive point is obtained of just 0.34Ω at 1.17Mc/s. Given the very similar minimum |Z| characteristics of both F_S and F_S2, when tuned respectively to the primary with corresponding values of C_S, either the fundamental or 2^nd harmonic could be used to operate the coil in experiments to explore MWO operation and effects.

Figures 3 below show the Z₁₁ impedance characteristics of the calibrated reference plane, the drive coil, and the primary and secondary tuning with series added capacitance, of the drive coil with the MWO top-load.

Fig. 3.1 Same wideband Z11 impedance characteristics for the TC drive now including the MWO topload. The fundamental M1 has moved down significantly from 1.28Mc/s to 650kc/s and is also quite strongly suppressed. The 2nd harmonic has strengthened, and the other higher harmonics remain mostly unchanged.
Fig. 3.2 Narrowband detailed impedance scan for the fundamental resonant frequency, 2nd, and 3rd harmonics.
Fig. 3.3 Cs = 400pF which represents a higher impedance at lower frequencies, and almost entirely suppressing the fundamental resonance.
Fig. 3.4 Cs = 570pF a slight increase, (previously 540pF without the MWO), in series capacitance in the primary in order to match the primary resonance with the secondary 3rd harmonic.
Fig. 3.5 Cs = 1300pF again a slight increase, (previously 1200pF without the MWO), in series capacitance in the primary in order to match the primary resonance with the secondary 2nd harmonic.
Fig. 3.6 Cs = 26000pF a very large increase, (previously 6500pF without the MWO), in series capacitance in the primary in order to match the primary resonance with the secondary fundamental.

Fig 3.1. Shows the wideband scan for the drive coil with MWO top-load on the same horizontal and vertical scaling as in Figures 2. The top-load at lower frequencies represents a considerable capacitive load at the top of the coil, very similar capacitively to a toroidal, cylindrical, spherical, or sheet metal top-load added to a conventional Tesla coil apparatus. The frequency of this scan is too low to show any of the high frequency features that result from the resonant rings of the MWO, (see part 2 for these features), but the capacitive loading of the MWO top-load could be clearly seen in this lower frequency scan. The biggest effect is noted at M₁ at F_S1 the fundamental resonance of the secondary which has reduced from 1.28Mc/s to 650kc/s, a 49.2% reduction . The 2^ndand 3^rd harmonics at F_S2 and F_S3 respectively have also reduced but in a much smaller range than the fundamental. F_S2 has reduced from 2.96Mc/s to 2.84Mc/s a 4.1% reduction, and F_S3 from 4.32Mc/s to 4.21Mc/s a 2.5% reduction. Higher harmonics also reduce with progressively reducing amounts up to F_S12 at M₁₂ which reduces from 16.51Mc/s to 16.46Mc/s a 0.3% reduction. It can be seen for this arrangement of drive coil the fundamental resonant frequency would be very sensitive and easily effected by metal loading to the top end of the secondary, the close proximity of metallic structures, or even to the proximity of partially conducting mediums such as the human body.

Fig 3.2. The narrowband scan shows the large change in the fundamental in relation to the 2^ndharmonic both in frequency shift and in the magnitude of the impedance and phase change. The MWO top-load has considerably quenched the fundamental of the drive coil, whilst leaving the 2^nd harmonic very similar to the coil only results (Figures 2) both in frequency and the magnitude of the impedance and phase.

Fig 3.3. Series capacitance C_S = 400pF as before shows the primary resonance in the band, but in this case has completely quenched the already weak fundamental resonance. It can be seen that driving the MWO at the 2^nd harmonic during experiments and operation may lead to considerably more stable and reliable system characteristics.

Fig 3.4. Shows the primary tuned at F_S3 at M₄ at 4.20Mc/s and a slightly increased series capacitance required to tune, increased from 540pF to 570pF.

Fig 3.5. Shows the primary tuned at F_S2 at M₃ at 2.83Mc/s and again a slightly increased series capacitance required to tune, increased from 1200pF to 1300pF. It can be noted that the fundamental resonance F_S can now just be discerned at M₁ at 650kc/s.

Fig 3.6. Shows the primary tuned at F_S at M₂ at 0.65Mc/s with F_L = 610kc/s and F_U= 700kc/s. The primary is tuned when C_S = 26000pF (26nF) which is a very large increase on the 6500pF required without the MWO top-load. At F_L(M₁) the impedance seen by the generator in the primary is now 0.61Ω which is no-longer the lowest driving impedance. With C_S = 1300pF and tuned to F_S2 the driving impedance at F_L2 is 0.47Ω which indicates that better power transfer from the generator to the secondary could be effected by driving the MWO at the 2^nd harmonic. At this point the system would also be more stable and less effected by proximity of metal structures and other partially conductive mediums including the human body.

The lower frequency impedance measurements have shown a wealth of frequency harmonics associated with the Tesla style drive coil, and can be tuned progressively with the primary of the drive coil via series capacitance to make use of the system at different designed resonant frequency points. The MWO top-load at lower frequencies introduces a considerable capacitive load on the drive coil which has a large quenching effect on the fundamental resonant frequency of the system, and suggests a shift of optimal setup away from being driven at the fundamental and towards the 2^nd harmonic where greater transference of electric power should be possible, and the system would be more stable and tolerant of loading conditions on the drive coils, the MWO top-load directly, and also from proximity of other conducting and partially conducting mediums. It will be interesting to determine if this changes when both the transmitter and receiver are combined in the full Lahkovsky MWO system, and also whether these effects can be directly demonstrated through experiments in the operation of the complete MWO system.

Click here to continue to part 2 of the multiwave oscillator impedance measurements.

1. Dollard, E., Design and presentation of an optimised and balanced MWO power supply and drive coils., Energy, Science, and Technology Conference (ESTC), 2018.

2. Vril Science, Lahkovsky Multiwave Oscillator, 2019, Vril

Lahkovsky MWO, Measurements

Multiwave Oscillator Impedance – Part 2

10th February 2019

In part 2 of the multiwave oscillator impedance (MWO) measurements we take a look at the high frequency impedance characteristics Z₁₁ for the MWO resonator rings (top-load). The MWO Tesla style drive coil measured in part 1 needs to be separated from the MWO top-load for this type of measurement, because the impedance and load of the drive coil masks out any resonant features at higher frequencies, making it impossible to measure the MWO when connected to the top of the secondary coil and measured at the input to the primary coil.

Experiments, operation, and measurements in Tesla coil based systems, and indeed in my own research regarding the displacement and transference of electric power, are normally limited to experimental apparatus which operates at maximum in the HF band < 30Mc/s of the electromagnetic spectrum. At 30Mc/s the corresponding wavelength λ is 10m. As a standard rule of thumb in high frequency or RF measurements the feature size of the element under measurement should be < λ/10 to be considered as a discrete lumped element in the system, and therefore not subject to impedance transformations through transmission line characteristics or other distributed network characteristics. At the upper end of the HF band this means that active measurement regions < 1m in size or length can be considered to have only small, if any, transformation and change on the impedance outside of that attributed with its discrete lumped element network.

As we progress to higher frequency measurements in the VHF band (30 – 300Mc/s) and even above in the UHF band (300Mc/s – 3Gc/s) very great care needs to be taken regarding the length and size of cabling and connections, the feature sizes of components within the measurement network, the impedance match or mismatch between transmission line sections and discrete components, and any other stray, parasitic, or proximity effects arising from boundary conditions that are both metallic or dielectric in nature. Accordingly, much greater care and attention needs to be taken to calibrate as accurately as possible directly to the plane of measurement, and then to normalise out measurement effects between the calibration plane and measurement apparatus.

In this part we are concerned with measurement up to ~1Gc/s (λ = 30cm), and where the λ/10 length is only 3cm. At λ/4 quarter-wavelength we would expect to see a complete impedance transformation along a transmission line from a very low impedance (short-circuit) at the output of the source generator to a very high impedance (open-circuit) at the end of a wire or measurement plane. Accordingly we need to keep connections small and efficient which represents in itself a unique challenge when connecting to the MWO rings, which at UHF frequencies represent a large distributed network of inter-connected transmission line elements, with complex boundary conditions. Subsequent parts will look at the MWO rings as an antenna with corresponding radiation resistance and defined radiation pattern and particularly in relation to the transmitter – receiver configuration of the complete MWO system.

For this part, and to measure as accurately as possible Z₁₁ for the MWO rings directly, and up to frequencies in the order of ~1Gc/s, it was necessary to make a connecting jig that allowed for extension of the reference plane from the VNA-SDR directly to the mounting spheres of the outer driven ring of the MWO. Figures 1 below show the measurement setup, signal feed adapter, MWO mounting jig, calibration elements, and overall arrangement of the high frequency impedance measurement apparatus.

Fig. 1.1 Experimental setup for the high frequency Z11 impedance measurements for the MWO rings, showing the VNWA-SDR, signal feed adapter, mounting jig, and calibration elements.
Fig. 1.2 Detail of the SFA and mounting jig showing connection between the input terminals and the brass mounting bolts. The effects of these connection elements are normalised out in the calibration plane.
Fig. 1.3 Mounting jig with a calibration element fixed in place, and intended to move the calibrated reference plane directly to the MWO connection point.
Fig. 1.4 MWO rings mounted to the jig after calibration.
Fig. 1.5 The measurement path was improved in the calibration by removing the SMA cable between the VNWA-SDR, and the SFA.
Fig. 1.6 The final measurement setup that produced the cleanest and most reproducible impedance scans.

To view the large images in a new window whilst reading the explanations click on the figure numbers below.

Fig 1.1. Shows the overall measurement setup with the VNA-SDR connected to the MWO mounting jig by a short SMA terminated RG316 cable, and the other end to the signal feed adapter (SFA), and standard calibration elements.

Fig 1.2. The SFA mounts directly to high voltage terminals, that are themselves connected to the brass mounting bolts used to hold the MWO rings to the jig. The jig is constructed predominantly in nylon 66 with a wooden internal support for strength inside the main jig support column. The high frequency path length and connection effects are normalised out by extending the calibration reference plane right to the brass bolt mounting points for the MWO outer ring. The SFA in this case is used with shorted series capacitance feed, and is balanced with equal weights of copper on the positive and negative feed paths, which includes the SMA connectors and the RG316 cable to the VNA-SDR. Equal weights of copper, or more accurately at high frequencies (> 3Mc/s), equal volumes of copper assist in balancing the boundary conditions for the electric and magnetic fields of induction and so reducing impedance mismatches in the signal feed path. As for part 1 an SFA with 3Gc/s balun was also tried but found to be largely unsuccessful in the small signal measurements due to the masking of high frequency detail, which results from the balun coupling transformer dominating the frequency characteristics in the mid to high-band frequencies.

Fig 1.3. The calibration elements fit directly onto the end of the MWO brass mounting bolts. With no element attached the mounts are calibrated for open-circuit, a single-sided pcb element is used for the short-circuit, and a single-sided pcb with 50Ω surface mount resistor in the centre for the calibrated load.

Fig 1.4. Shows the MWO rings mounted to the measurement jig.

Fig 1.5. An improvement to the calibration procedure removed the SMA connecting cable by mounting the VNA-SDR directly to the SFA by SMA coupler. In this configuration some additional resonant features were removed from the normalised calibration results.

Fig 1.6. The final measurement setup for the high frequency MWO impedance measurements with VNA-SDR directly mounted to the SFA, which is in turn directly mounted to the jig, and where the calibration plane is at the point where the MWO outer ring brass balls meet the brass mounting bolts.

Figures 2 below show the Z₁₁ impedance characteristics of the calibrated reference plane and the lower high frequency measurement band 100kc/s – 500Mc/s. The entire high frequency band was split into two in order to best comply with the calibration bands within the VNA-SDR instrument. At 500Mc/s the instrument internally changes reference method and level, and sensitive measurements cross-band are not recommended. Therefore the measurements are calibrated into a lower band 100kc/s-500Mc/s and an upper band 500Mc/s – 1.3Gc/s.

Fig. 2.1 Calibration scan over the lower band for the 50Ω reference load, showing two points of interest at M2 and M4 which may need to be factored out of the detail for the measured results at these points.
Fig. 2.2 Lower high frequency band scan showing a wealth of resonant structure that results predominantly from the outer rings of the MWO top-load. Markers are positioned on the 12 lower features of interest.
Fig. 2.2 Same lower high frequency band scan showing marker points at the 12 upper points of interest.

Fig 2.1. Calibration for the 50Ω reference element over the band. Markers M₁, M₃, and M₅ show the consistent calibration across most parts of the band. At M₂ at 138Mc/s and M₄ at 377Mc/s there are resonances within the calibrated signal path which are too significant to normalise out. These points will need to be factored into the measurement results to remove features of interest, if any, that correspond at these frequencies. At these 2 points features in the results are considered measurement artefacts that arise due to the measurement system and inter-connection between the instrument and the MWO rings at the calibration plane.

Fig 2.2. Shows the rich range of resonant features that result from the MWO rings and their inter-action across the band. In this first result markers M₁– M₁₂ are used to identify the lower 12 set of features, and in the next set of results the upper 12 set of features. There is no corresponding feature at 138Mc/s as seen in the calibration scan, and hence this point does not need to to be removed from the results. The first 250Mc/s of the results show a number of strong resonant points indicated by the large phase changes occurring at M₄, M₆, M₈, and M₉, and most likely attributed to resonances in the outer few rings of the MWO. There are also smaller phase inversions across the first half of the results occurring at M₁, M₂, M₅, M₇, M₁₀, and M₁₁ which most likely arise due to resonant inter-actions between the outer few rings of the MWO. At M₁₂ 287Mc/s a large peak change in |Z₁₁| occurs for a very small phase inversion, which would likely indicate where the outer drive ring of the MWO becomes self-resonant, in a similar way to that of the primary in the drive coil which becomes self-resonant at ~38MC/s. The point at M₁₂ may also correspond to the 2^nd harmonic of this point with the fundamental occurring at M₈, this however being less likely due to the very low impedance swing at M₈ to ~6.9Ω indicating that M₈ is more likely to be associated with the fundamental resonance of one of the few outer rings, but not the driven ring.

Fig 2.3. Shows the markers on the upper 12 set of features. At M₁₀ 375Mc/s there is a large resonance, the only in the upper 250Mc/s of the results, which also very closely corresponds to the calibration feature noted in Fig 2.1. at M₄ at 377Mc/s. The close correspondence of these two points means that the feature at M₁₀ needs to be attributed to a strong resonance in the calibration path which could not effectively be normalised out by the calibration procedure. Otherwise in the upper part of the results there are some small phase inversions at M₁₁ and M₁₂ which could be tentatively linked to the fundamental resonant frequencies of some the rings further into the MWO centre. In the upper part of the results we start to see a general masking, smearing, and suppression of further detail, not necessarily because the detail is not there, but rather the coupling between rings is not sufficiently loose to allow for the natural resonance of each ring to be reflected in the results, and combined with rapidly increasing losses, large reductions in Q, and decreasing amplitude of oscillation as the results move towards the centre of the MWO. This could be further tested and measured by decreasing the coupling factor between each of the rings by changing the structure of the MWO from a flat set of rings to a cone configuration, where each of the rings retain the same diameter but are separated further apart vertically on the cone yielding a three-dimensional MWO structure. The other way to measure and assess this further is to remove every other ring in the flat MWO so reducing the coupling between rings and also reducing the large number of inter-active resonances. The process of starting with one ring inside the driven ring and subsequently adding ring by ring taking an impedance scan with each ring, would also assist in clarifying which fundamentals occur from which rings, and which features occur due to cross-coupling between the rings.

Figures 3 below show the Z₁₁ impedance characteristics of the calibrated reference plane and the upper high frequency measurement band 500Mc/s – 1.3Gc/s.

Fig. 3.1 Calibration scan for the upper band using the 50Ω reference, and showing good consistency over the band up to marker M3 at ~ 1.1Gc/s.
Fig. 3.2 Upper band results showing some features in the lower section markers M1 - M5.

Fig 3.1. The calibration of the upper high frequency band shows very good consistency and results for the 50Ω reference load up to M₃ at 1096Mc/s. Above this point the signal attenuation is such that the returned measurement currents to the VNA-SDR are so small as to be falling outside the lower dynamic range of the instrument, and hence the results become progressively more inaccurate and noisy. It is to be noted that the base 50Ω reference load can still be extrapolated visually to the end point ar 1300Mc/s. However, above ~1Gc/s the results on this measurement apparatus and setup are considered to not be of further use as can be more clearly seen in the next result.

Fig 3.2. At the lower end of this band markers M₁ – M₅ continue the upper band of the previous results in most likely showing fundamental resonances and maybe even some inter-actions between some of the more inner rings of the MWO e.g. rings 4-7. It is unlikely that any details can easily be discerned for the inner rings 8-11 where the signal reflections are very small, and stronger coupling between rings has largely smeared out the detail and suppressed the Q of the response.

Overall the high frequency impedance measurements have presented a wealth of detail particularly in the lower part of the band and with discernible results being contributed to by as many as the first 6-8 rings inside the outer driven ring. It is also clear that cross-coupling between rings will contribute to very high frequency components to be emitted from the MWO, even though such detail is largely outside of the scope and dynamic range of the measurement technique used here. A useful comparison measurement would be to look at the range of frequency components generated during normal high tension operation of the complete MWO system, using a spectrum analyser instrument with capabilities into the Gc/s range. The high frequency impedance characteristics still need to be measured for the complete MWO system where both transmitter and receiver are connected to the system, which will be reported in a subsequent part.

1. Vril Science, Lahkovsky Multiwave Oscillator, 2019, Vril