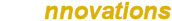The Wheelwork of Nature – GU5B VTTC and High Voltage Supply Updates
ESTC 2023 – The Golden Ratio-Dragon Discharge and The Burning-Bush Flame Speaker
At the 2023 Energy, Science, and Technology conference[1] in Spokane USA, AMInnovations gave several detailed and extensive presentations on The Golden Ratio Discharge[2], The Toltec System of Knowledge[3], a combined presentation with Eric Dollard and Aaron Murakami on the Ultra Low Frequency Amplifier Modulator[4] (The Burning-Bush Flame Speaker), and a Panel Discussion[5] on Tesla related technology and phenomena. The full official ESTC video presentations and demonstrations can be purchased directly from A & P Electronic Media, and a preview of these presentations are shown below. The AMInnovations presentations in pdf format as presented at the conference can be downloaded using the following links, The Golden Ratio Discharge, and The Toltec System of Knowledge.
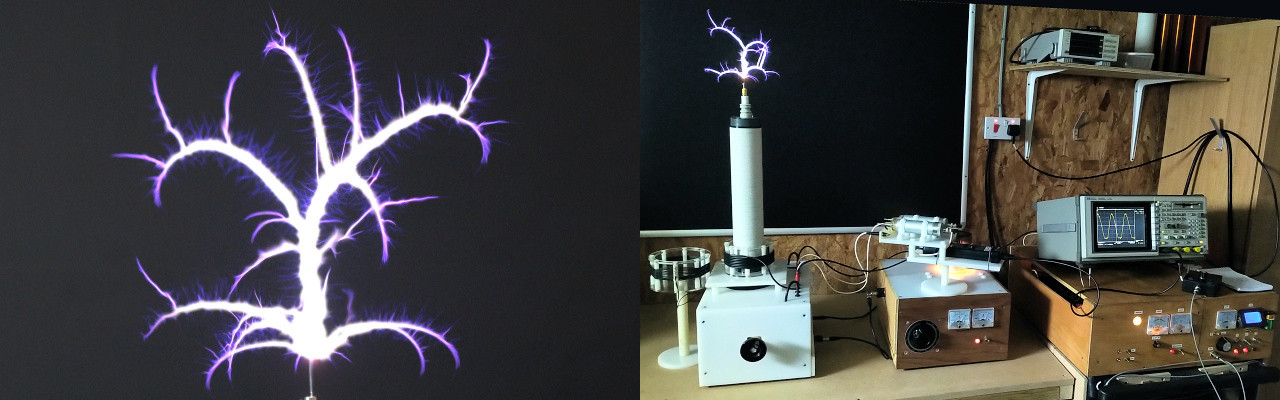
The Golden Ratio is one of the fundamental underlying principles in the Wheelwork of Nature, and is reflected within many forms in the natural world. The Golden Ratio Discharge reflects this fundamental principle in the field of electricity and energy, first discovered by Eric Dollard in 1978, and now rediscovered by Adrian Marsh, and demonstrated by using a specific arrangement of Tesla coil and generator. The ESTC 2023 presentation makes an in-depth exploration of this unique discharge, looking into its scientific, engineering, and philosophical/esoteric origins, and how to practically reveal this discharge in a Tesla coil system, as well as considering its importance as an example of a core underlying principle of nature revealed in the field of electricity and electro-magnetism.
A complete engineering apparatus and schematics are disclosed for the experimental Tesla coil system, along with comprehensive measurements of the power supply, generator, and Tesla coil characteristics in both the time and frequency domain. The presentation contains all the necessary design keys to replicate this remarkable experiment. Vibration, tuning, and resonance of the experiments are explored in detail, and how to transition the discharge form from the Golden Dragon, a fractal expanding with Golden Ratio proportions, to more conventional Sword streamers. The Golden Dragon discharge shows profound symmetry, temporal and spatial coherence, and a choreography that demonstrates in no uncertain terms the fundamental nature of this underlying principle of the natural world.
The inner nature of the Golden Ratio discharge is explored using high-speed photography up to 2000 times which shows the creation and extinction of each discharge streamer, and hidden within this the first conjectured emergence of ball-lightning, or the formation of a “micro-sun”, the precursor to an inclusive fusion process, observed before within specialised vacuum tubes, but never before manifested in free-space. The presentation concludes with a live demonstration of the optimal tuning of the experimental apparatus to generate the Golden Ratio discharge in the form of the Golden Dragon, and then through specific tuning and adjustment the transition to sword streamers at lower frequencies.
The Golden Ratio Discharge experiment in this presentation is shown to support Tesla’s profound statement, “… then it is a mere question of time when men will succeed in attaching their machinery to the very wheelwork of nature.”, and has the potential to reveal deeper insights, principles, and knowledge of the natural order.
The Toltec System of Knowledge is a vast system of experiential knowledge acquired over aeons upon aeons of time, and handed down from one generation to another only through oral and experiential training. The word Toltec simply means “a man or woman of knowledge”, and is independent of race, gender, religion, country, language, or any other differentiating factors within humanity. The Toltecs have systematically developed and evolved their knowledge of life and the universe, often quietly behind the scenes, and far from the normal daily pursuits of the world.
The Toltecs have long understood that the outer-world is but a reflection of the diversity and richness of our inner-world. Modern science is currently a good description of the form of the natural world, in other words the outer-world, what things are made-of, and how these forms interact with one-another on the outside, the what, where, and the how of the physical form. The Toltec system of knowledge goes beyond this outer form, and works with the inner-world, intelligence, awareness, perception, and the hidden knowledge and understanding, the why, purpose for, and meaning of life’s most fundamental principles.
The practical application of the Toltec system of knowledge grows you awareness, and can transform your life far beyond your present comprehension. When we each contribute to the growth of humanity’s collective awareness, we will bring about a more inclusive, inter-dependent, and life-supportive approach, and a multidisciplinary understanding of our-self, each other, and the natural world. Little known or understood, this presentation introduces this system of knowledge, who the Toltecs are, and what they have accomplished through studying the great mystery and problems of the physical and spiritual universes.
AMInnovations has been pioneering in research, innovation, and invention for almost four decades in science, technology, and computing, both within conventional science and the new science. He has a Ph.D. in Physics from the Cavendish Laboratory, Cambridge University, where he undertook several years of ground-breaking research in superconducting coherent quantum effect devices. Core fields of current research include Tesla Energy and Electricity research, Quantum Device Physics, Coherent Low-Level Laser Holistic Medical devices, and Esoteric Science and Medicine. Adrian has replicated many of Eric Dollard’s fundamental Tesla based experiments in electricity, and also rediscovered the Golden Ratio Discharge using a specialised Tesla coil apparatus. His day-to-day research activities are orientated to the discovery of the underlying principles and processes within the Wheelwork of Nature, including Telluric Power Transmission, Non-Linear Open Energy Systems, Displacement and Transference of Electric Power, and Esoteric Energetic Systems. Adrian’s research is self-funded and by donations through the not-for-profit organisation AMInnovations, and is supported by The Foundation for Toltec Research.
1. ESTC 2023, Energy, Science, and Technology Conference, A & P Electronic Media , 2023, ESTC
2. Marsh A. The Golden Ratio Discharge, A & P Electronic Media, 2023, EMediaPress
3. Marsh A. The Toltec System of Knowledge, A & P Electronic Media, 2023, EMediaPress
4. Dollard E., Marsh A., Murakami A. Ultra Low Frequency Amplifier-Modulator, A & P Electronic Media, 2023, EMediaPress
5. Marsh A et al. Panel Discussion 2, A & P Electronic Media, 2023, EMediaPress
6. A & P Electronic Media, AMInnovations by Adrian Marsh, 2019, EMediaPress