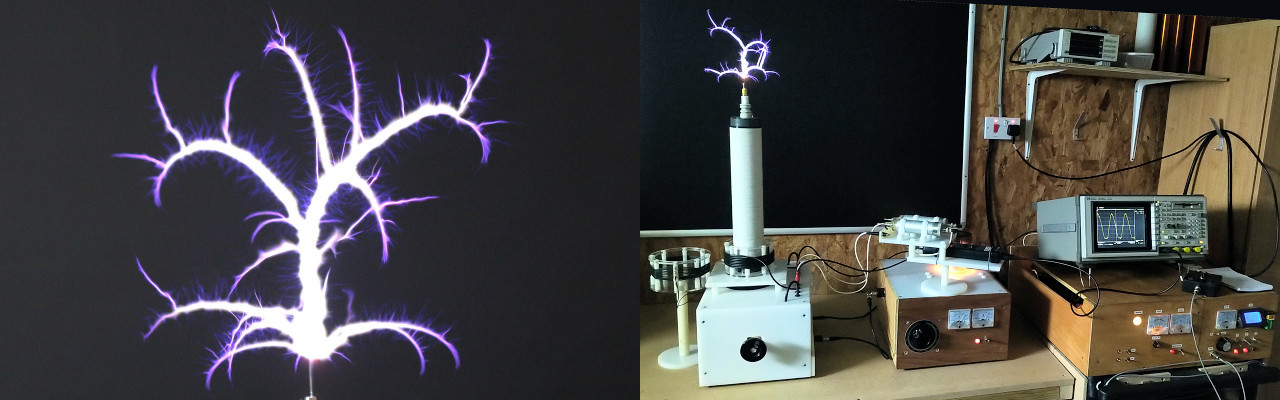
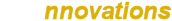Sooner or later research into the underlying nature and principles of electricity must inevitably lead to those larger philosophical and esoteric questions surrounding the origin and purpose of life, its mechanisms that constitute the wheelwork of nature, and our purpose and part to play as very small cogs in this grand design. I have in previous posts started to tentatively touch-on and develop my own current understanding of the wheelwork of nature through ideas, designs, experiments, and conjectures regarding displacement and transference of electric power. This post is the first in a sequence looking at experiments in electricity which reveal or suggest clues about this underlying wheelwork, with the associated phenomena and results, their possible origin and purpose, and how we may form a synchronicity with this wheelwork, and hence benefit from a journey that increases our knowledge and awareness of our-self and that of the great mystery or grand design. This first post in the series looks at the wheelwork of nature - Golden Ratio or Fractal "Fern" Discharge experiment, along with observations, measurements, and interpretation ... Read post
Tesla’s Radiant Energy and Matter Featured Article Sticky
Some of the most fascinating areas of research into the inner workings of electricity, are those that display unusual and interesting phenomena, and especially those not easily understood and explained by mainstream science and electromagnetism. The field surrounding Tesla's radiant energy and matter, the apparatus, experiments, and wealth of unusual electrical, and even non-electrical related phenomena, is a particular case to note. This first post in a sequence serves as a practical and experimental introduction to this area, along with consideration and discussion of the observed phenomena, and possible interpretations as to their origin and cause. It is through working to understand these types of phenomena, often generated in high tension, unipolar, and non-linear electrical systems such as the Tesla coil and TMT transmission system, that the inner workings of electricity can be revealed little by little. That is to say, the outer workings of electromagnetism that account for almost all of those measurable electrical properties that constitute the transference of energy, and hence electric power, between source, load, and the intervening transmission medium, can be peeled back to show a more fundamental, coherent, and guiding mechanism ... Read post
Telluric Transference of Electric Power – MF Band 27-70 Miles Featured Article Sticky
This experimental post is a follow on from the field-work reported so far in Telluric Transference of Electric Power - MF Band 2-8 Miles and Transference of Electric Power – Single Wire vs Telluric. In this new experiment the same TMT apparatus and generator is used at 1.86 Mc and 400W of transmit power, and the telluric transmission medium is extended into the far-field region at 27 and 70 mile field locations from the TX coil. At the 27 mile location a natural lake was used as the telluric ground connection for the RX coil, and the transmitted signal could just be received, and was shown to result from the combination of a telluric-wave component through the ground, and a radio-wave component above the ground. At the 70 mile location the sea was used as the telluric ground connection, but despite many different combinations of configuration, tuning, measurements, and instruments, the transmitted signal could not be received either through the telluric-wave or the radio-wave. The dominant transmission mode in these experiments appears to be Transverse Electromagnetic (TEM), and it is conjectured that in the more distant far-field a three coil TMT arrangement using Tesla's extra coil may be necessary to "pull" or "draw" the transmitted signal through the coherent cavity via the Longitudinal Magneto-Dielectric (LMD) transmission mode ... Read post
High-Efficiency Transference of Electric Power Featured Article Sticky
In this post we take a preliminary experimental look at the transference of electric power using a cylindrical coil TC and TMT, energised using a linear amplifier generator, and also the high power transfer efficiency that can be achieved in a properly matched system. The setup, tuning, and matching of the linear amplifier is covered in detail in the video experiment where a 500W incandescent lamp can be fully illuminated at power transfer efficiencies over 99% in the close mid-field region. The power is shown to be transferred to the receiver through a single wire between the transmitter and receiver coil through the longitudinal magneto-dielectric mode, and not through transverse electromagnetic radiation or through direct transformer induction. This high-efficiency, very low-loss transference of electric power is possible as the dielectric and magnetic fields of induction are contained around the single wire ... Read post